An ideal on a set X is a non-empty collection of subsets of X with heredity property which is also closed under finite unions. The concept of nearly compact spaces was introduced by Singal and Mathur (1969). This paper introduces nearly compact spaces with respect to an ideal and discusses some of their properties.

Given a non-empty set X, a collection of subsets of X is called an ideal:

1) If and implies (Heredity)

2) If and implies (Additivity)

If then is called a proper ideal.

An ideal is called a ideal if the following holds: If {An: n = 1, 2, …...} is a countable sub-collection of , then {An : n = 1, 2, ….}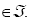

The notation denotes a non-empty set X, a topology on X and an ideal on X. Given point denotes the neighborhood system of x, i.e., . The symbol denotes collection of all subsets of X. Given space and a subset A of X, we define for every .

Computational Mathematics Journal, Compact Spaces, Heredity Property, Neighborhood System, Kuratowski Closure Operator, Topological Spaces, Continuous Surjection, Hausdorff Space, Countable Subsets, Closed Sets.